Session 1 - getting started with BXA

This session introduces how to construct a BXA fit to spectra in a variety of different setups.

Key objectives:

  • Fit a spectrum with BXA in Sherpa and/or PyXspec
  • Interact with posteriors
  • Fit more than one spectrum simultaneously with BXA

To start with, make sure you import the relevant packages:
  • PyXspec: 
    from xspec import *
import bxa.xspec as bxa
     
  • Sherpa: 
    import bxa.sherpa as bxa
     

Exercise 1.1 - prior predictive checks

Prior predictive checks are used to see if the priors chosen can lead to realistic model realisations.
Note for these exercises, setting priors in BXA is done with the following commands:
Also, log uniform priors cannot be zero or negative. Make sure the parameter ranges you supply are positive.

To start with, we will fit the NuSTAR data alone. First load the data, notice the correct energies and create model1 based on a powerlaw (see the commands in Exercise 0.1 for help). Note the target in question can be assumed to be at redshift 0.05 with a Galactic column density of NH = 4×1020 cm-2:
  • PyXspec:
    model1 = Model("TBabs*zpowerlw")
model1.TBabs.nH.values = (0.04, -1.) ## Milky Way absorption
model1.zpowerlw.PhoIndex = (1.8, 0.1, -3., -2., 9., 10.)
model1.zpowerlw.Redshift.values = (0.05, -1.)
model1.zpowerlw.norm.values = (1.e-4, 0.01, 1.e-10, 1.e-10, 1., 1.)
     
  • Set the parameter priors for model1 (note norm varies over many orders of magnitude, and PhoIndex can be assigned a uniform prior for now):
  • A note on log parameters (Sherpa only): Using a loguniform prior may not give the posterior values of that parameter in log units in Sherpa.
    Instead, the Parameter module can convert a parameter to log units, and then one can use a uniform prior for that parameter. E.g.:
    from sherpa.models.parameter import Parameter
logpar = Parameter(modelname, parname, value, min, max, hard_min, hard_max)
model1.norm = 10**logpar
     
    • Note the parameter will only be valid for working in BXA. If you want to define a log parameter and use this with a standard Sherpa fit, the log parameter must appear in the model expression.
  • Create a solver:
    • PyXspec:
      solver = bxa.BXASolver(transformations=[prior1, prior2], outputfiles_basename="model1_nu")  
    • Sherpa:
      solver = bxa.BXASolver(prior=bxa.create_prior_function([prior1, prior2]),
                       parameters=[param1, param2],
                       outputfiles_basename="powerlaw_sherpa")
       
    Make sure:
    1. outputfiles_basename is always unique. Especially if running PyXspec and Sherpa in the same directory.
    2. (For Sherpa) the priors are in the same order for the prior and parameters attributes.

  • Perform prior predictive checks:
    1. Generate a random sample of prior parameter values (remember to import numpy!):
      • PyXspec:
        values = solver.prior_function(numpy.random.uniform(size=len(solver.paramnames)))  
      • Sherpa:
        values = solver.prior_transform(numpy.random.uniform(size=len(solver.paramnames)))  
    2. Set the parameters to these values:
      • PyXspec:
        from bxa.xspec.solver import set_parameters
set_parameters(transformations=solver.transformations,values=values)
         
      • Sherpa:
        for i, p in enumerate(solver.parameters): p.val = values[i]  
    3. Plot the resulting prior model realisation with the data:
      • PyXspec:
        Plot("ldata")  
      • Sherpa:
        plot_fit(xlog=True, ylog=True)  
    4. Repeat 100 times, and plot the prior realisations with the data. Are the model ranges covered by the priors physically-acceptable?


Exercise 1.2 - fit a model to a spectrum

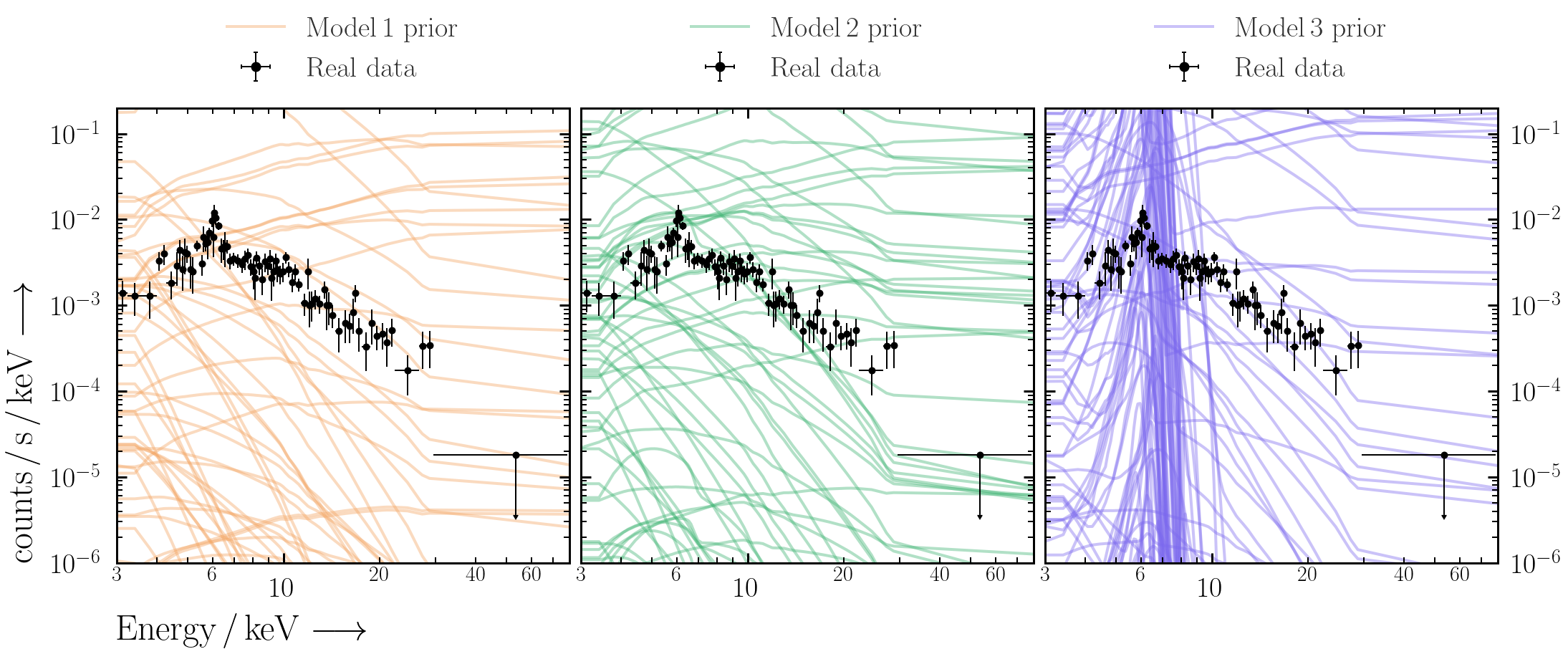
Now that we have checked the priors look reasonable for the data we want to fit, we can fit the model to the data with BXA and get parameter posteriors.
  • First fit the model using Levenberg-Marquardt included in Xspec & Sherpa:
    • PyXspec:
      Fit.perform()  
    • Sherpa:
      fit()  

  • Is the fit good? How can you tell? What does changing the parameters by a small amount do?

  • Next perform the fit with BXA (note this does not require fitting with Levenberg-Marquardt first):
    • PyXspec:
      results = solver.run(resume=True)  
    • Sherpa:
      results = solver.run(resume=True)  
    (Note the hyperlinks are different).
    results contains the posterior samples (results["samples"]) for each parameter and the Bayesian evidence (results["logZ"], results["logZerr"]). These quantities should also be printed to the screen after the fit is completed.
    To understand more about the information UltraNest prints to the screen during and after a fit, see here.

  • Examine the best-fit values and uncertainties from the posterior samples. This can be done with pandas (may require installing with e.g., conda install pandas but see warning at the end of Setup):
    import pandas as pd
posterior_df = pd.DataFrame(data=results["samples"], columns=solver.paramnames)
posterior_df.to_csv("%s/posterior.csv" %(outputfiles_basename), index=False)
      

  • How do the best-fits and confidence ranges compare with using nested sampling vs. Levenberg-Marquardt?

  • Finally, save the best-fit model (which is loaded as the current model by default with BXA) set-up to enable restoring it easily at later stages:
    Xset.save("%s/model.xcm" %(outputfiles_basename))
      


Exercise 1.3 - fit different models

Next fit an additional two models to the data (which are used in subsequent exercises). Make sure to perform prior predictive checks each time before fitting.

  • model2 features the same powerlaw as in model1 but with additional photo-electric absorption:
    • PyXspec:
      model2 = Model("TBabs*zTBabs*(zpowerlw)")
model2.TBabs.nH.values = (0.04, -1.) ## Milky Way absorption
model2.zTBabs.Redshift.values = (0.05, -1.)
model2.zTBabs.nH.values = (1., 0.01, 0.01, 0.01, 100., 100.)
model2.zpowerlw.PhoIndex.values = (1.8, 0.1, -3., -2., 9., 10.)
model2.zpowerlw.Redshift.link = "p%d" %(model2.zTBabs.Redshift.index)
model2.zpowerlw.norm.values = (1.e-4, 0.01, 1.e-10, 1.e-10, 1., 1.)
       

    Use the same priors as for model1 with an additional loguniform prior for zTBabs.nH.
  • model3 features the same absorbed powerlaw as in model2 but with an additional Gaussian line:
    • PyXspec:
      model3 = Model("TBabs*zTBabs*(zpowerlw+zgauss)")
model3.TBabs.nH.values = (0.04, -1.) ## Milky Way absorption
model3.zTBabs.Redshift.values = (0.05, -1.)
model3.zTBabs.nH.values = (1., 0.01, 0.01, 0.01, 100., 100.)
model3.zpowerlw.PhoIndex.values = (1.8, 0.1, -3., -2., 9., 10.)
model3.zpowerlw.Redshift.link = "p%d" %(model3.zTBabs.Redshift.index)
model3.zpowerlw.norm.values = (1.e-4, 0.01, 1.e-10, 1.e-10, 1., 1.)
model3.zgauss.LineE.values = (6.4, 0.1, 6., 6., 7.2, 7.2)
model3.zgauss.Sigma.values = (1.e-3, 0.01, 1.e-3, 1.e-3, 1., 1.)
model3.zgauss.Redshift.link = "p%d" %(model3.zTBabs.Redshift.index)
model3.zgauss.norm.values = (1.e-5, 0.01, 1.e-10, 1.e-10, 1., 1.)
       

    Assume a uniform prior for zgauss.LineE and loguniform priors for zgauss.Sigma and zgauss.norm.

Exercise 1.4 - error propagation

By generating quantities directly from the posterior samples, we propagate the uncertainties and conserve any structure (e.g., degeneracies, multiple modes).
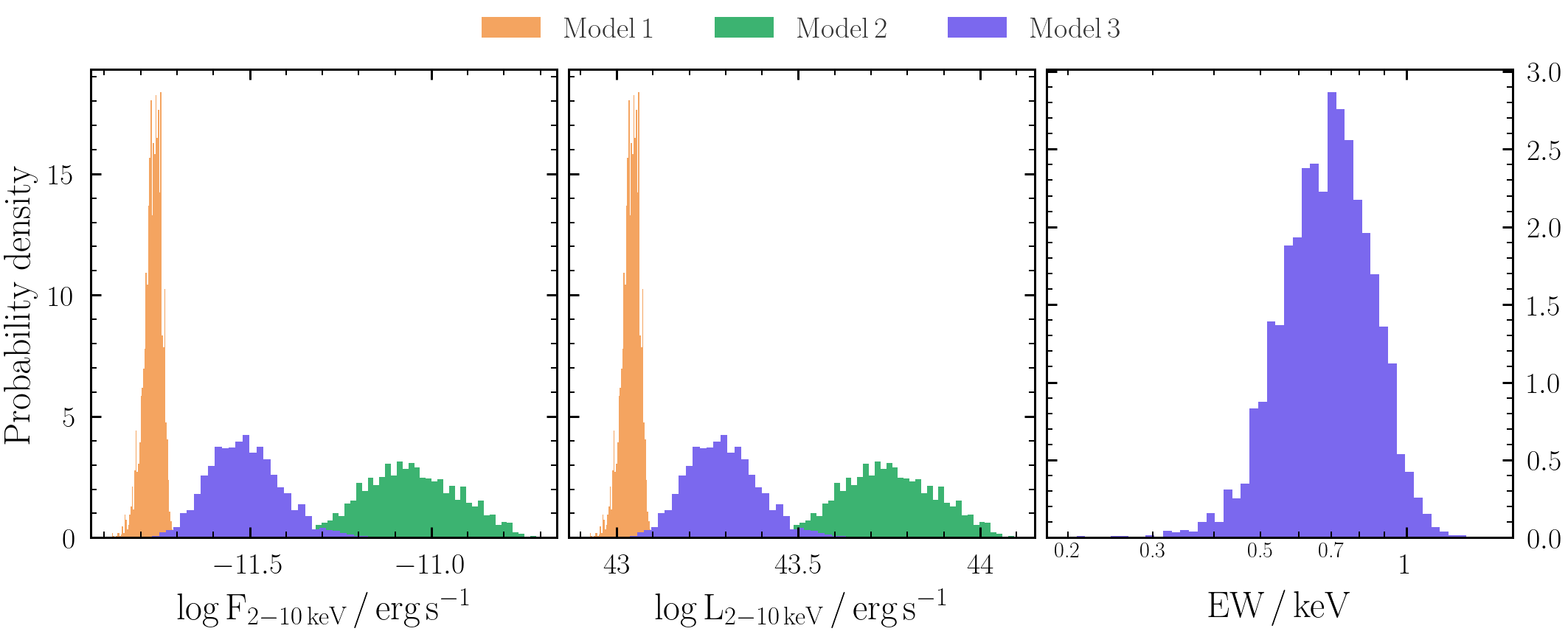
We will consider three examples for posterior-based error propagation. Note the example code uses a posterior_df pandas dataframe to propagate the uncertainties.
  • Unabsorbed powerlaw flux: To calculate the flux of the powerlaw model component, we multiple by energy and integrate between Emin_keV=2 and Emax_keV=10. Make sure to convert the units of the powerlaw normalisation so we get flux in erg/s/cm2.
    ## note have to be careful if PhoIndex ~ 2
if numpy.isclose(PhoIndex, 2., atol = 1.e-2):
    logflux = lognorm + numpy.log10(numpy.log(Emax_keV / Emin_keV))
else:
    A = 2. - PhoIndex
    logflux = lognorm + numpy.log10(((Emax_keV**A) - (Emin_keV**A)) / A)
     
  • Unabsorbed powerlaw luminosity: Now we have the unabsorbed flux, and we know the source is at redshift 0.05 we can estimate the distance and thus the luminosity. 
    from tqdm import tqdm
z = 0.05
from astropy.cosmology import FlatLambdaCDM
chosen_cosmology = FlatLambdaCDM(H0=67.3, Om0=0.315)
D_cm = chosen_cosmology.luminosity_distance(z).value*(10**6)*(3.086*10**18)
tqdm.pandas(desc="Calculating logluminosity in the 2-10 keV band")
posterior_df.loc[:, "loglum"] = posterior_df["logflux"].progress_apply(lambda x: x + numpy.log10(4.*numpy.pi) + 2.*numpy.log10(D_cm))
     
  • Unabsorbed equivalent width: The equivalent width (EW below) of an emission line is defined as the flux in the line divided by the flux of the continuum at the line energy (see the Xspec documentation for more information). By considering just the zpowerlw> and zgauss components (i.e. no absorption), we get the unabsorbed equivalent width.
    EW_keV = ((10 ** lognorm_zgauss)/(10 ** lognorm_zpow))*(LineE**PhoIndex) / (1.+z)
     

  • Are any of the secondary parameters you have derived degenerate with the original parameters?

  • How do the unabsorbed flux and equivalent width posteriors compare between different models?

  • Extension: load a fixed number of posterior model rows into Xspec and calculate the observed flux and equivalent widths. How do the observed (i.e. absorbed) model fluxes and equivalent width posteriors compare to the unabsorbed values derived above?


Exercise 1.5 - fitting multiple datasets simultaneously with BXA

Sometimes it is advantageous to fit multiple spectra for the same source simultaneously with a cross-calibration constant to account for instrumental differences associated with the separate spectra.

For this example, we need another dataset. As an example, we will use the Chandra/ACIS spectrum included in the downloadable files which will be fit in the energy range 0.5-8 keV to extend our spectral range to lower energies than attainable with just NuSTAR.

We first assume that the source was not variable between the NuSTAR and Chandra observations, and thus only account for differences arising from the calibration of either instrument with an additional factor pre-multiplying each spectrum.

  • First, include a cross-calibration constant in your model between the Chandra and NuSTAR datasets:
    • PyXspec:
      AllData("1:1 nustar_src_bmin5.pha 2:2 chandra_src_bmin5.pi")
AllData.ignore("1:0.-3. 78.-** 2:0.-0.5 8.-**")

model1 = Model("constant*TBabs*zpowerlw")
AllModels(1).constant.factor.values = (1., -1.)
AllModels(1).TBabs.nH.values = (0.04, -1.) ## Milky Way absorption
AllModels(1).zpowerlw.PhoIndex.values = (1.8, 0.1, -3., -2., 9., 10.)
AllModels(1).zpowerlw.Redshift.values = (0.05, -1.)
AllModels(1).zpowerlw.norm.values = (1.e-4, 0.01, 1.e-10, 1.e-10, 1., 1.)
AllModels(2).constant.factor.values = (1., 0.01, 0.1, 0.1, 10., 10.)
Plot("ldata")
       
    • Sherpa:
      load_pha(1, "nustar_src_bmin5.pha")
ignore_id(1, "0.:3.,78.:")
load_pha(2, "chandra_src_bmin5.pi")
ignore_id(2, "0.:0.5,8.:")
model1 = xstbabs.tbabs*xspowerlaw.mypow
x1model1 = xsconstant("xcal1") * model1
set_par(xcal1.factor, val=1, frozen=True)
x2model2 = xsconstant("xcal2") * model1
set_par(xcal2.factor, val=1, min = 1.e-2, max = 1.e2)
set_source(1, x1model1)
set_source(2, x2model2)
        

  • Fit the new model with BXA and derive a posterior confidence range on the cross-calibration constant. Remember to do prior predictive checks before fitting!
    Warning: fitting model3 with both datasets simultaneously can take up to an hour.

  • How have the confidence ranges on all the model parameters changed after including Chandra?

  • Have the uncertainties on unabsorbed flux or equivalent width changed?

Exercise 1.6 - (Sherpa only) automated background fitting with BXA

So far, the exercises have used modified C-statistics (aka W-statistics) in which the background is modelled as a stepwise function with the same number of parameters as bins. This process typically requires some form of minimal binning (see discussion here).

Using C-statistics can be more flexible, since no binning is required by simultaneously fitting a background model instead. Here we use the auto_background function in BXA, which provides a powerful way to implement background models in Sherpa, and simultaneously fit with a source model using BXA.

Contact