Why use BXA?
Key strengths:
- Systematic fitting with minimal user input of initial parameters
- Efficient to systematically fit large datasets with many sources or compare many models
- Provides accurate parameter constraints, even for (very) low counts or for complex parameter spaces with strong degeneracies
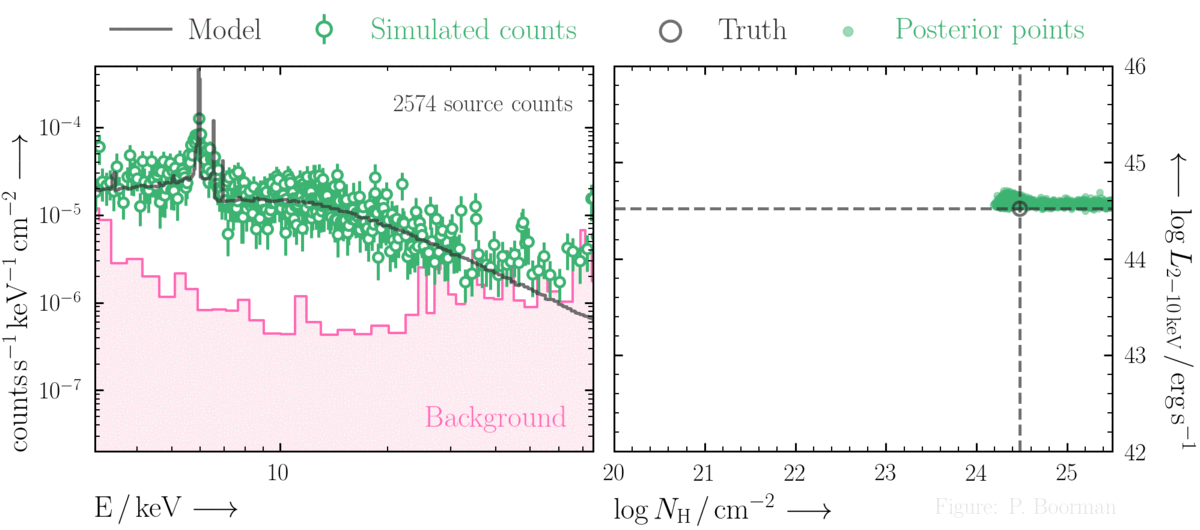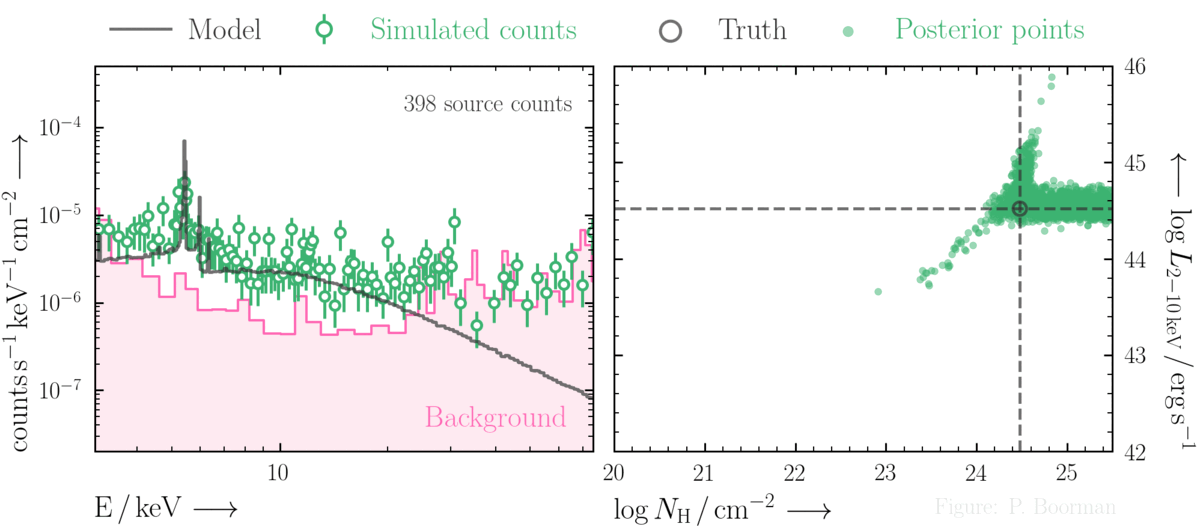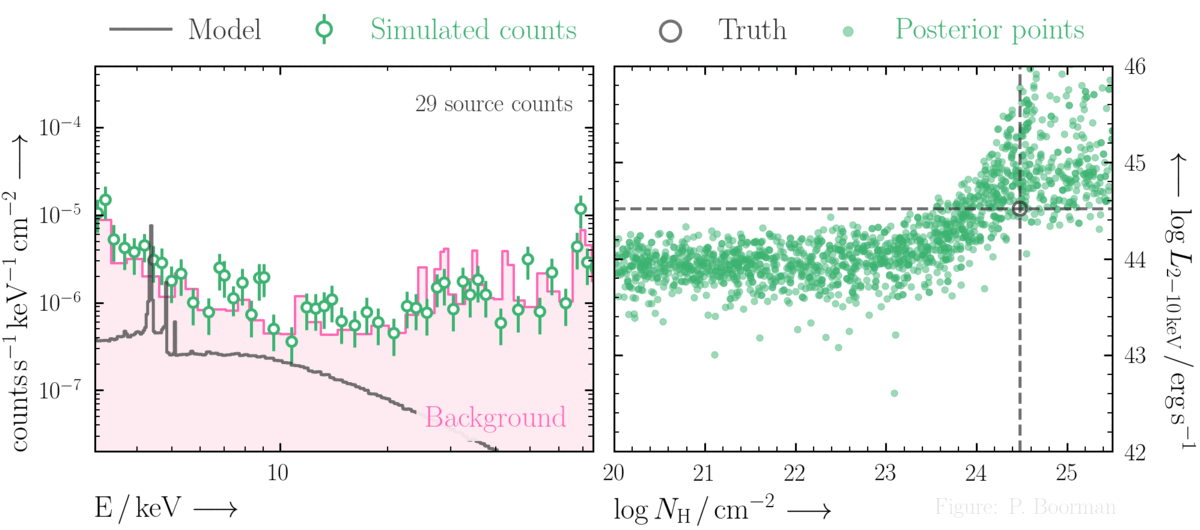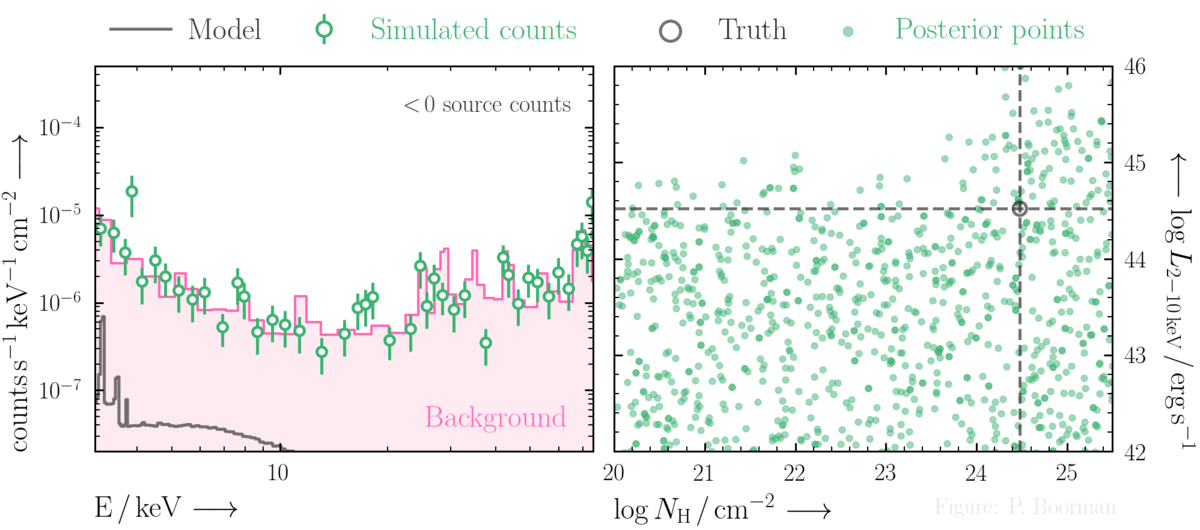
Parameter space constraints in the (very) low count regime
BXA is capable of accurately estimating parameter confidence contours, even when no source counts are present. In this figure, a series of obscured accreting supermassive black hole (ak AGN)
spectra are simulated (left panel). The right panel then shows the BXA_derived confidence contours for intrinsic line of sight obscuring column density (log NH) vs. intrinsic
(i.e. unabsorbed) X-ray luminosity in the 2-10 keV band.
By simultaneously fitting the background and source spectra, BXA is able to derive a confidence contour for low count spectra even down to zero source counts (though the constraint is very poor,
as expected). The contour found makes sense, since an unobscured AGN (i.e. log NH ~ 20) should have been detected if it were very bright. This is why the upper left portion of
the contour plane is always ruled out.
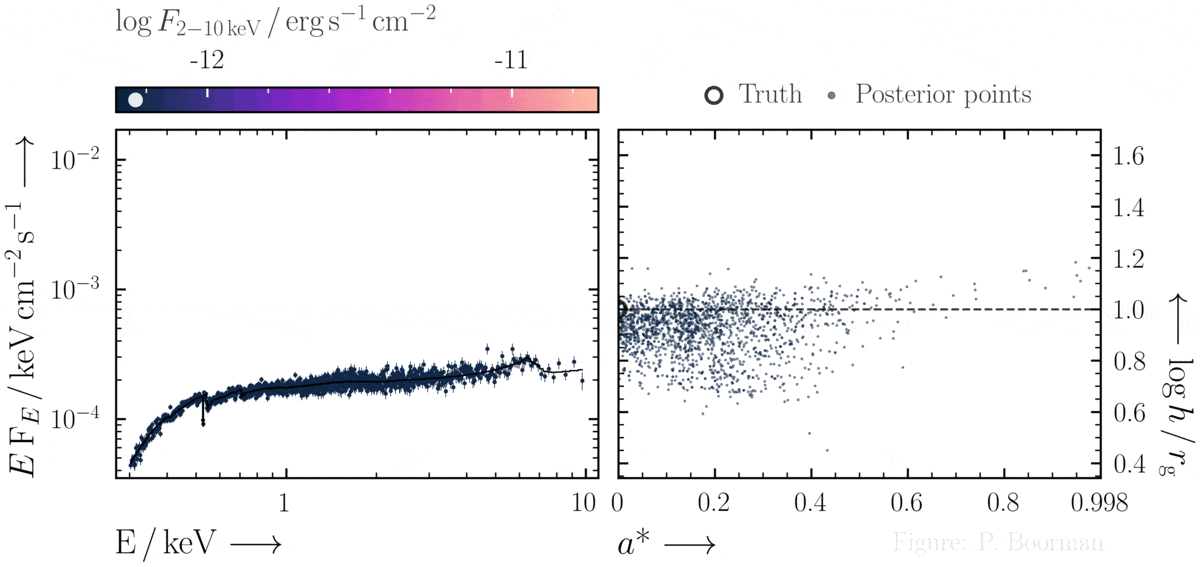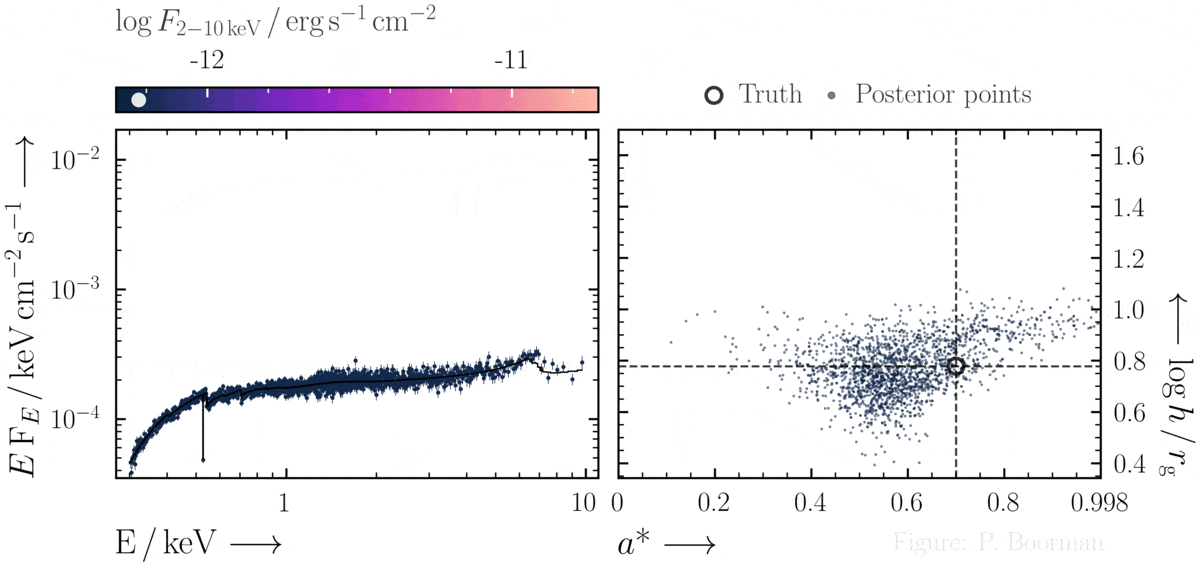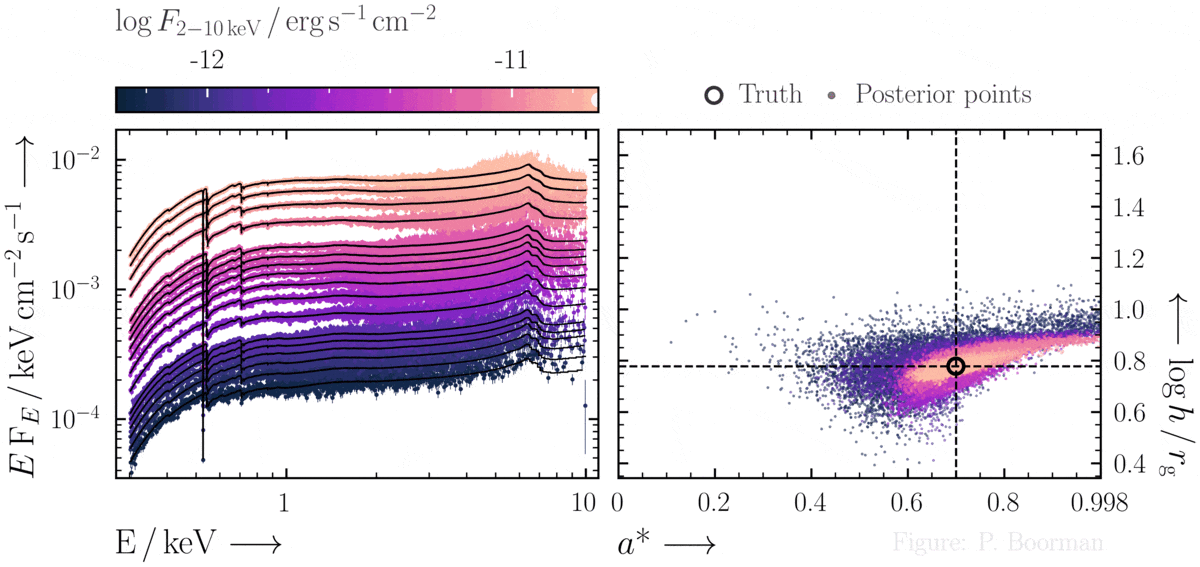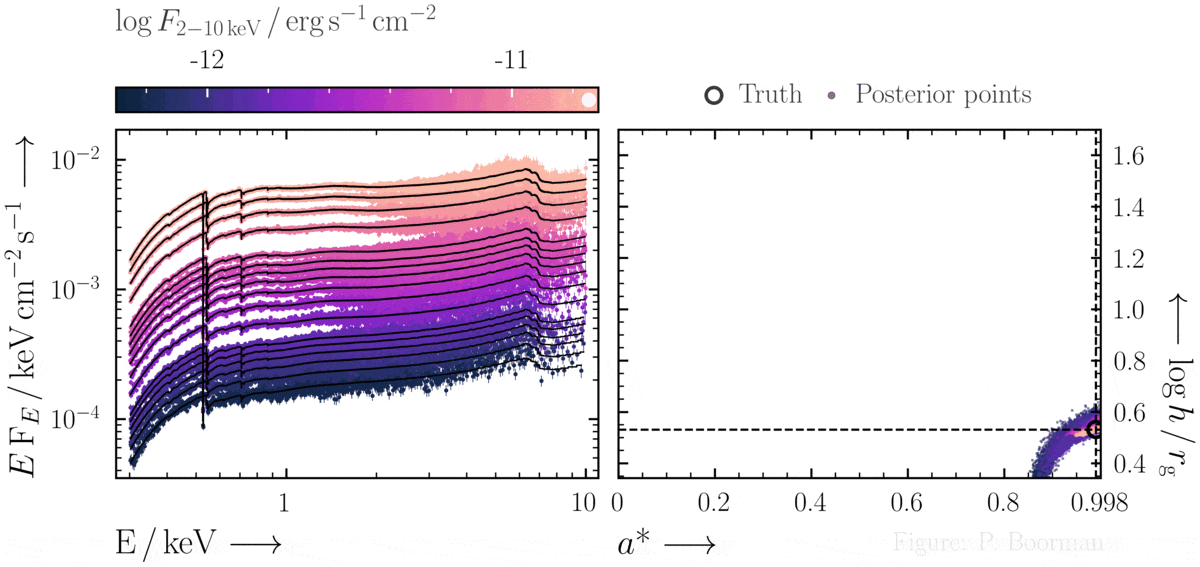
No need for fine-tuning initial parameters
BXA does not require a single pre-defined position in the parameter space to start exploring. In this figure, a series of X-ray spectra are simulated at incrementally brighter fluxes. The right panel shows the confidence contour between two parameters in the simulations - black hole spin vs. the height of the X-ray emitting source above the black hole (assuming the lamp post geometry). Both parameters were assigned uninformative priors before fitting over a wide range of possible values. The size and shape of the confidence contours found are thus independent of any single initial parameter values.